等しい比

　　等しい比を見つけよう

等しい比

等しい比を見つける問題場面の把握が的確にできます。

→

小学校

算数

６年

　デジタルコンテンツ提示による等しい比を見つける問題場面において、２つの比が等しいわけ、図や言葉、計算を使って説明することによって、比が等しいことの意味を理解する。

　２つの比が等しいといえるわけを、図や言葉を用いて説明できるようになる。

同じ味はどれ　問題提示　動画

問題提示に用い、課題追求することにより、大きさのちがう入れ物を使ってカフェオレを作っても、同じ味のものは、量の比が同じであることを絵や図を用いて説明できるようにする。また、□対△の両方に同じ数をかけたり、両方の数を同じ数でわったりすると同じ比ができることを、発見させる。

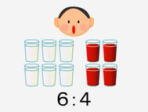
主な活動

指導上の留意点

１　問題提示のあと、問題を把握する。

「３人がそれぞれカフェオレを作りました。それぞれ量は違いますが、ミルクとコーヒーの割合が同じであれば、味も同じになるはずですね。３人が作ったカフェオレのうち同じ味のものはどれでしょう。」

　コンテンツ１　課題部分
　

カフェオレの味は、ミルクとコーヒーの混ざり具合で決まります。３人のカフェオレの味を比べられるように、図に書いてみましょう。

　・もとの入れ物の図で表してみよう。
　・取り分けたコップの中身を線分図で表してみよう。
　・もとの入れ物とコップの中身の関係を表してみよう。
　・数字の大きさを比べてみよう。

２．自力解決をする。　　

どの比が同じか。理由をつけた説明をノートに書こう。

・３本の線分図で考える。
・コップを１として、分数で考える。
・数をもとに倍関係で考える。
・比がちがうのはちがうのは、なぜかを説明する。

３．各自の考え方を発表し、検討する。

比が同じというのは、どのように説明できるのだろうか。

「６：２と３：４のコップは、味が同じ。」
「同じ入れ物にして比べたときに、中身の割合が同じこと」
「６：２＝３：４と言える。これを比が等しいという。」

４．教科書の適応題をする。

・動画で問題を提示したあと、３人のカフェオレの作り方についてキャプチャ画面を印刷したものを、比較検討する資料として掲示する。

　　　　　　　　　コンテンツ１　部分掲示

・どんな図や表し方を使って考えを書けばよいか、支援する。
・作るときの入れ物の大きさにかかわらず、同じ単位の入れ物何倍分と何倍分と考えると、味はコップ一杯の中身の混ざり具合で見ることに注目させたい。
・コップ一杯を１として、それを、部分比に分ける考え方も出て来るであろう。
・数字に着目して、６：４と３：２の関係を説明する考えも出て来るであろう。
・一部の児童には、７：３と他の２つとの違いを、図で説明できないかを考えさせたい。

・線分図で考えれば、コップ一杯分はどれも同じ大きさになることを押さえる。
・等しい比の比の倍関係に着目した考えにも、注目させる。

・比が同じということの、いろんな説明の仕方にな得できるかを評価する。
・等しい比の書き表し方を知らせる。

・等しい比の意味とともに、等しい比の書き表し方を理解できたかを評価する。

授業場所	■教室　□特別教室　□体育館　□運動場　□屋外　　□その他［　　　　　］
授業形態	■一斉学習　□グループ学習　□個別学習　□補習　　　□その他［　　　　　］
ＩＴを活用する場面	■導入　■展開　□まとめ　□その他［　　　　　］
ＩＴを主に活用する者	■教員　□学習者　□両方　□その他［　　　　　］
ＩＴを主に活用する目的	■課題の提示　■動機付け　■教員の説明資料　　　□学習者の説明資料　□繰り返しによる定着　　　■モデルの提示　□失敗例の提示　□体験の想起　　　□比較　□振り返り　□体験の代行　□その他［　　　　　］
活用するＩＴ	■コンピュータ　■プロジェクタ　■スクリーン　　　□電子ホワイトボード　□実物投影機　□デジタルカメラ　　　□ビデオ　■インターネット　□デジタルコンテンツ　　　□ＣＤ－ＲＯＭ　□スピーカー　□その他［　　　　　］